Halo teman-teman, pada artikel ini akan membahas mengenai mengenai materi volume benda putar. Bagaimana cara menghitung volume benda putar dengan menggunakan integral tentu, yuk simak materinya.
B. Volume Benda putar
Apa yang disebut volume? Kita mulai dengan benda-pejal sederhana yang disebut silinder tegak, empat diantaranya diperlihatkan pada Gambar 1. Dalam tiap kasus, benda itu dibentuk dengan cara menggerakkan suatu daerah rata (alas) sejauh `h` dengan arah tegak lurus pada daerah tersebut. Dan dalam tiap kasus, volume benda-pejal didefinisikan sebagai luas alas dikalikan tinggi , yakni:
`V=A.h`
(Gambar 1)
Berikut perhatikan sebuah benda-pejal yang penampang-penampangnya tegak lurus dengan suatu garis memiliki luas yang diketahui. Khususnya, misalkan garis tersebut adalah sumbu -`x` dan misalkan bahwa luas penampang pada `x` adalah `A(x)` dengan `a≤x≤b` (Gambar 2). Kita partisikan interval `[a,b]`dengan menyisipkan titik-titik `a=x_0<x_1<x_2<...<x_i=b`. Kemudian kita lewatkan bidang-bidang melalui titik-titik ini tegak lurus pada sumbu - `x`, sehingga mengiris benda menjadi lempengan-lempengan tipis (Gambar 3). Volume suatu lempengan kira-kira sama dengan volume `\Delta V`
(Gambar 2). (Gambar 3)
(Gambar 6)
(Gambar 7). (Gambar 8)
(Gambar 9)
Benda putar yang sederhana dapat kita ambil contoh adalah tabung dengan besar volume adalah hasil kali luas alas (luas lingkaran) dan tinggi tabung. Bila luas alas dinyatakan dengan `A(x)` dan tinggi benda putar adalah panjang selang `[a,b]`, maka volume benda putar dapat dihitung menggunakan integral tentu sebagai
Untuk mendapatkan volume benda putar yang terjadi karena suatu daerah diputar terhadap suatu sumbu, dapat dilakukan dengan menggunakan tiga buah metode, yaitu metode cakram, metode cincin dan metode kulit silinder.
Bila daerah yang dibatasi oleh `x=f(y)≥0, x=g(y) ≥ 0, f(y)≥g(y)` untuk setiap `y € [a,b], x=c` dan `x=d` diputar terhadap sumbu - `y`, maka volume :
(Gambar 10)
(Gambar 11)
suatu silinder, yakni:
`\Delta V_i=A(\overline {x_l}) \Delta x_i`
(Ingat bahwa `\overline{x_i}` disebut titik sampel, adalah sebarang bilangan dalam interval. Volume V dari benda-pejal dapat diaproksimasikan dengan jumlah Riemann
`V\approx \sum_{i=1}^{n} A(\overline{x_l}) \Delta x_i`
Ketika norma partisi mendekati nol, diperoleh integral tertentu yang didefinisikan sebagai volume benda-pejal `V=\int_{a}^{b} A(x)dx`
a. Pemutaran mengelilingi Sumbu X
Misal R adalah luasan yang dibatasi oleh `y=f(x), x=a,x=b` Selanjutnya R diputar mengelilingi sumbu - `x` . Lintasan kurva karena mengelilingi sumbu - `x` membentuk bangun berupa benda padat (pejal), yang dapat diiris menjadikan lempengan-lempengan. Volume `\Delta V` suatu lempengan kira-kira sama dengan volume suatu silinder, yakni:
`\Delta V_i=A(\overline{x_l}\Delta x_i`
Volume V dari benda-pejal dapat diaproksimasikan dengan jumlah Riemann:
`V\approx \sum_{i=1}^{n} A(\overline{x_l}) \Delta x_i`
Ketika norma partisi mendekati nol, diperoleh integral tertentu yang didefinisikan sebagai volume benda-pejal
`V=\int_{a}^{b} A(x)dx`
`V=\int_{a}^{b} π(y^2) dx=π \int_{a}^{b} y^2 dx`
(Gambar 4). (Gambar 5)
Jika dibatasi oleh dua kurva, yaitu `y_1=f(x), y_2=g(x), x=a, x=b`. Dengan Selanjutnya R diputar mengelilingi sumbu - `x` , maka terbentuk benda-pejal yang volumenya dapat didekati dengan menggunakan integral tertentu, yaitu:
`V=π \int_{a}^{b} (y_{1}^{2} -y_{2}^{2}) dx`
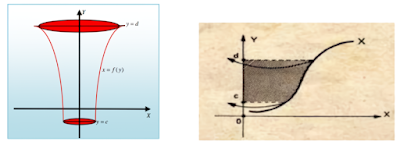
b. Pemutaran Mengelilingi Sumbu Y
Misal R adalah luasan yang dibatasi oleh `x=f(y), y=c, y=d` . Selanjutnya R diputar mengelilingi sumbu - `x`. Lintasan kurva akan membentuk bangun berupa benda pejal. Benda tersebut volumenya dapat didekati dengan menggunakan integral
tertentu yaitu:
`V=π \int_{a}^{b} x^2 dy`
Jika R dibatasi oleh dua kurva, yaitu `x_1=f(y), x_2=g(y), y=c, y=d`. Dengan `x_1≥x_2`. Selanjutnya diputar mengelilingi sumbu - `x`, maka terbentuk benda pejal yang volumenya dapat didekati dengan menggunakan integral tertentu, yaitu:
`V=π \int_{c}^{d} (x_{1}^{2} -x_{2}^{2}) dy`
berikut:
`V=\int_{a}^{b} A(x) dx`
1. Metode Cakram
Misal daerah dibatasi oleh `y=f(x), y=0, x=1`dan `x=b` diputar terhadap sumbu - `x` . Volume benda-pejal/padat yang terjadi dapat dihitung dengan memandang bahwa volume benda-pejal tersebut merupakan jumlah tak berhingga cakram yang berpusat di titik-titik pada selang `[a,b]` .
Misal pusat cakram `(x_0,0)`dan jari-jari `r=f(x_0)` Maka luas cakram dinyatakan :
`A(x_0) =π(f(x_0))^2 =πf^2 (x_0)`
Oleh karena itu, volume benda putar:
`V=\int_{a}^{b} π (f(x^2))^2 dx=π\int_{a}^{b}(f(x))^2 dx`
Bagaimana bila grafik fungsi mengelilingi sumbu -`y`? Apabila grafik fungsi dinyatakan dengan `x=g(y), x=0, y=c, y=d` diputar mengelilingi sumbu - `y`, maka volume benda putar :
`V=\int_{a}^{b} π (g(y))^2 dx=π\int_{a}^{b} (g(y))^2 dx`
Bagaimana bila pada dua kurva? Bila daerah yang dibatasi oleh untuk setiap diputar terhadap sumbu -`x` , maka volume :
`V=\int_{a}^{b} π (f(x))^2 - (g(x))^2 dx`
`V=\int_{c}^{d} π (f(y))^2 - (g(y))^2 dy`
Contoh:
Hitung volume benda putar bila luasan yang dibatasi oleh kurva-kurva:
`y=2-x^2, y=-x` dan sumbu - `y`bila diputar mengelilingi garis `y=-2`
Jawab
Kedua kurva berpotongan di `(-1,1)` dan `(-2,2)`. Pada selang `[-1,2]` berlaku `2-x^2 \geq-x` Jarak kurva `y=2-x^2, y=-x` terhadap sumbu putar (garis `y=-2`) dapat dipandang sebagai jari-jari dari cakram, sehingga diperoleh `\left(2-x^2\right)-(-2)=4-` `x^2` dan `-x-(-2)=2-x`. Maka berturut-turut adalah`\left(4-x^2\right)` dan `(2-x)`.
`\Delta V \approx \pi [(4-x^2)^2 -(2-x)^2] \Delta x`
`=\pi (x^4-9 x^2+4x+12) \Delta x`
`-1 \leq x \leq 2`
Sehingga diperoleh:
`V =\int_{-1}^2 \pi\left(x^4-9 x^2+4 x+12\right) d x`
`=\pi \int_{-1}^2\left(x^4-9 x^2+4 x+12\right) d x`
`=\pi\left[\frac{x^5}{5}-3 x^3+2 x^2+12 x\right]_{-1}^2=\frac{108}{5} \pi`
`V = \frac{108}{5} \pi \approx 67,86 \text { satuan volume }`
2. Metode Cincin
Metode cincin merupakan metode yang dibentuk oleh hasil putaran persegi panjang terhadap sumbu putaran tertentu (sumbu putaran tidak berimpit dengan sisi persegi panjang), seperti gambar berikut
Jika dan secara berturut-turut merupakan jari-jari dalam dan luar dari cincin dan tmerupakan ketebalan cincin, maka volumenya dapat ditentukan sebagai berikut.
`V=\pi (R^2-r^2)t`
Untuk mengetahui bagaimana konsep ini dapat digunakan untuk menentukan volume benda putar, perhatikan daerah yang dibatasi oleh jari-jari luar `R(x)`dan jari-jari dalam `r(x)`seperti yang ditunjukkan gambar di bawah ini.
Jika daerah tersebut diputar menurut sumbu putar yang diberikan, volume benda putar yang dihasilkan adalah
`V=\pi\int_{a}^{b} [(R(x))^2-r(r(x))^2]dx`
Contoh:
1. Tentukan volume benda putar yang dibentuk oleh putaran daerah yang dibatasi oleh grafik dari `y=x^2`, sumbu- `x` dan garis `x=2`diputar terhadap garis `y=-1`
Jawab
Jika irisan diputar terhadap garis `y=-1` akan diperoleh suatu cincin dengan jari-jari dalam 1 dan jari-jari luar `1+x^2`.
`\Delta V \approx \pi\left[\left(1+x^2\right)^2-1^2\right] \Delta x`
` =\pi\left(x^4+2 x^2\right) \Delta x`
`0 \leq x \leq 2`
Sehingga diperoleh,
`V =\int_0^2 \pi\left(x^4+2 x^2\right) d x`
`=\pi \int_0^2\left(x^4+2 x^2\right) d x`
`=\pi[\frac{x^5}{5}+\frac{2}{3} x^3]_0^2`
`=\frac{186}{15} \pi`
`V =\frac{176}{15} \pi \approx 36,86 \text { satuan volume}`
2. Hitung volume benda putar bila luasan yang dibatasi oleh kurva-kurva: `y=2-x^2, y=-x` dan sumbu- `y` bila diputar mengelilingi garis `y=-2`
Jawab
Kedua kurva berpotongan di `(-1,1)` dan `(-2,2)`. Pada selang `[-1,2]` berlaku `2-x^2 \geq-x`
Jarak kurva `y=2-x^2, y=-x` terhadap sumbu putar (garis `y=-2` ) dapat dipandang sebagai jari-jari dari cakram, sehingga diperoleh `(2-x^2)-(-2)=4-x^2` dan `-x(-2)=2-x` maka berturut-turut adalah `(4-x^2)` dan `(2-x)`.
`\Delta V \approx \pi[\left(4-x^2)^2-(2-x)^2\right] \Delta x`
`=\pi\left(x^4-9 x^2+4 x+12\right) \Delta x`
`-1 \leq x \leq 2`
Sehingga diperoleh,
`V=\int_{-1}^2 \pi(x^4-9 x^2+4 x+12) d x`
`=\pi \int_{-1}^2\left(x^4-9 x^2+4 x+12\right) d x`
`=\pi\left[\frac{x^5}{5}-3 x^3+2 x^2+12 x\right]_{-1}^2=\frac{108}{5} \pi`
`V=\frac{108}{5} \pi \approx 67,86 \text { satuan volume }`
Sekian materi volume benda putar, semoga teman-teman semakin paham yaaa.
